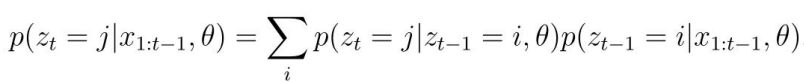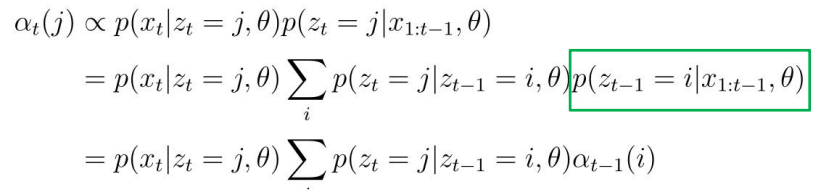C4 连续数据的生成模型
本文的部分公式格式未校对,正在施工中……
C4 连续数据的生成模型
生成分类器
在C2中,我们提到,生成模型也是一个分类模型,通过对离散变量的贝叶斯建模,可以得到 朴素贝叶斯分类器(NBC),事实上,这一点也可以推广到连续数据。只需将概率建模改为“类条件密度函数”:
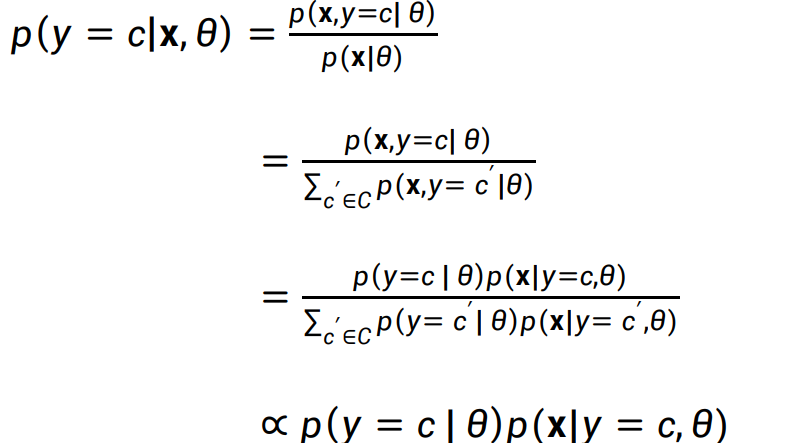
记好这个结论,在后面两节我们会使用其来训练一个** 多元高斯分布** 分类器
单一正态分布的高斯模型
这一节我们专注于高斯分布(正态分布),因为它是连续变量中的最常见的建模。
我们先一句带过 一元正态分布,对没错就是这个:
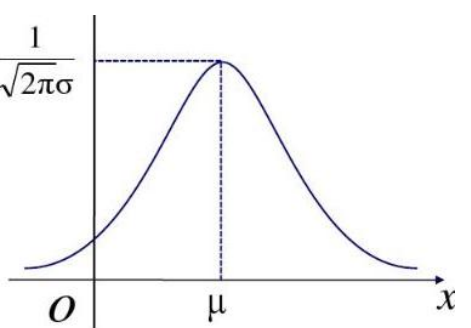
它的概率密度函数是,大家应该都知道吧。
实际上,多元连续变量也是具有正态分布的(概率论里其实也学过,不过大概大家都忘了):

其中,我们把 称为** 马氏距离 ,这是欧式距离在多元空间中的推广:**
下面我们提这样一个问题:给定N个独立同分布的样本,如何估计该多元高斯分布的参数呢?
同样,可以使用MLE和MAP两种估计方法。
- 极大似然估计
- 似然函数:
- 最大化时的参数结论:
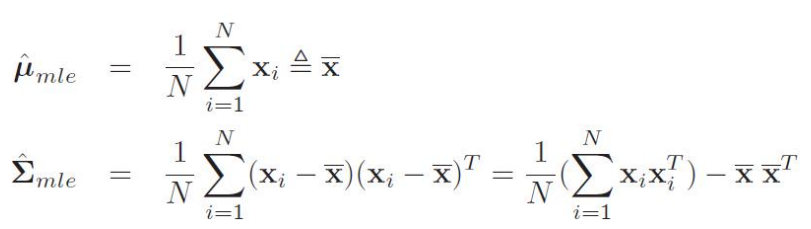
- 最大后验概率估计
- 似然函数
其中,对于,可以用采样数据x的均值和散度表示为:
,其中
- 最大化时的参数结论:
- 因为是MAP,需要引入先验的参数:
- ,即先验均值
- :对的信任程度 ,为0或一个极小值
- ,协方差的先验,并取平均
- :对的信任程度 ,,D是维度
- 然后对先验均值和极大似然估计的结果做** 凸组合 ,定义:**
- ,即先验均值
- 因为是MAP,需要引入先验的参数:
\bold m_N = \frac{k_0}{k_0+N}\bold m_0 + \frac{N}{k_0+N}\bar x \\ \
\\
\bold S_N = \bold S_0 + S_{\bar x} + \frac{k_0 N}{k_0+N}(\bar x - \bold m_0)(\bar x - \bold m_0)^T \\ = \bold S_0 + S_{\bar x} + k_0\bold m_0\bold m_0^T-K_N \bold m_N\bold m_N^T \\ \
\\ 其中:
k_N = k_0 + N \\
v_N = v_0 + N
则估计结果为:
- 
高斯判别分析
上一节我们已经学习了如何以 多元高斯分布 为随机变量建模贝叶斯生成模型,结合第一节所说,下面我们尝试利用其生成一个分类器。
假设我们有多个训练样本数据,它们对对应的类别分别是
那么可以定义当条件为“随机变量被分为类别c”的条件密度函数:
其中是 所有被分为类别c的训练样本数据构成的多元高斯分布 的 均值 和 协方差矩阵
按照生成分类器的 后验估计最大 为原则,和离散生成分类器的输出类似,可以得到分类的计算公式:
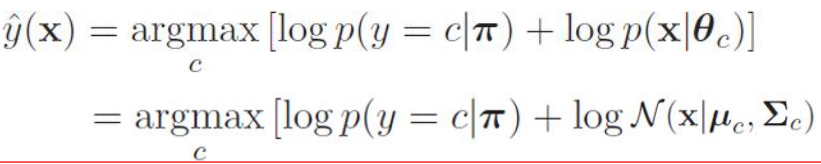
其中,是分类先验的分布
如果对于类别c,先验分布是均匀的 ,则推导公式为:
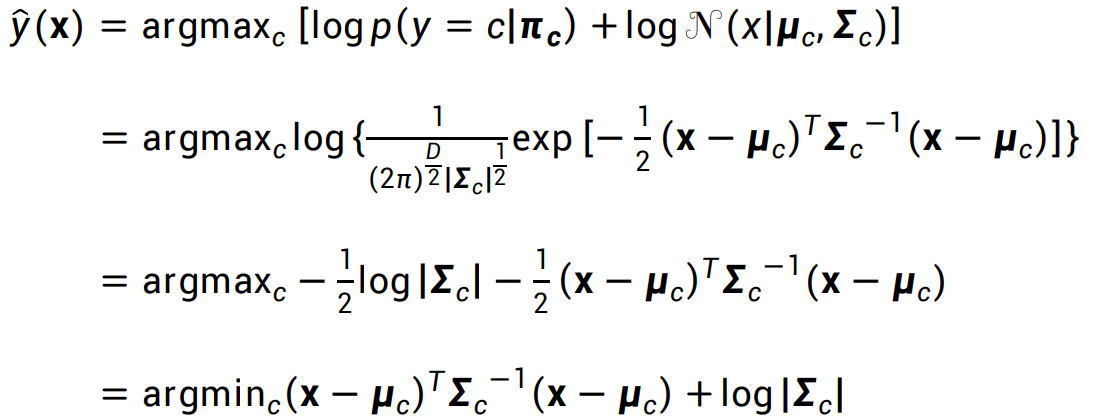
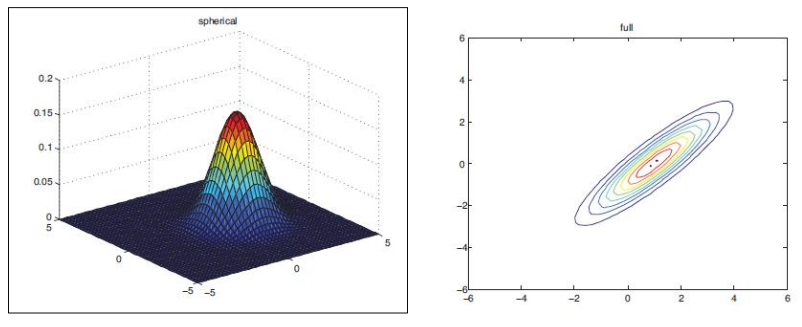
- 如果 x 是二元变量,那么y(x)的分类结果(决策边界)在平面图上会呈现一条二次曲线,因此,也将这种方法称为“二次判别分析”)下图是一个这样的例子:
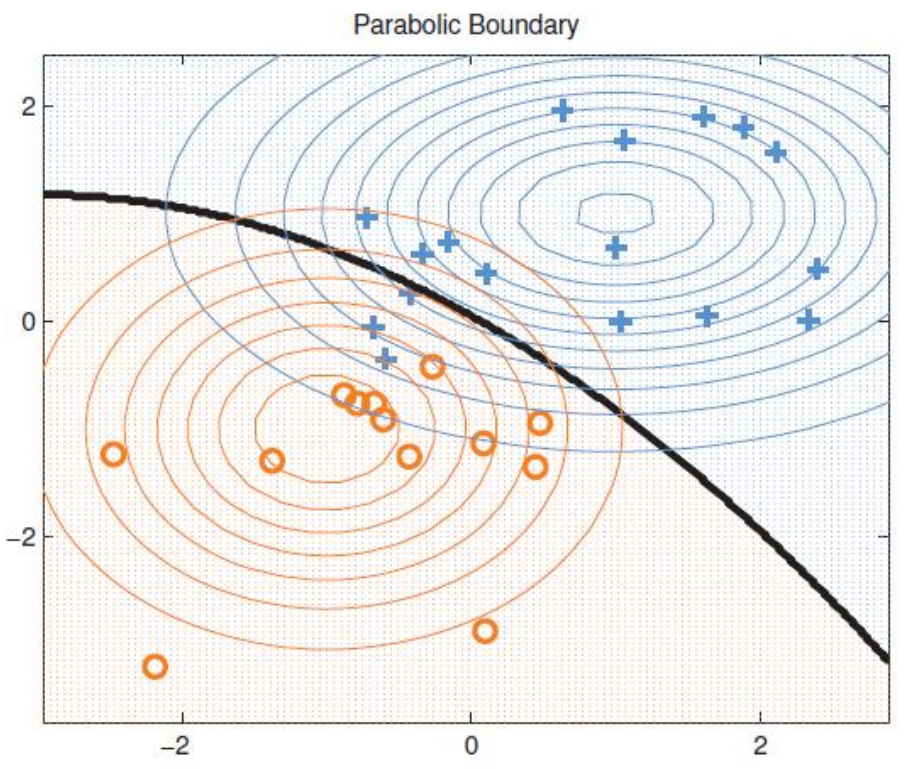
在这个图示中,样本变量x是一个二元的变量,因此被绘制在平面上,每个点还对应一个y值,图中的圆圈表示的是y值的等高线。
x相对y的值服从正态分布,直观地绘制出三维和二维的对比图,其实是这样的:
- 如果对于任意的类别c,有,则决策边界恰好是一条直线,此时“二次判别分析”退化为“ 线性判别分析 ”,可以直接写出决策线的表达式:
其中参数矩阵,,下图是一个这样的二元变量线性分类的例子:
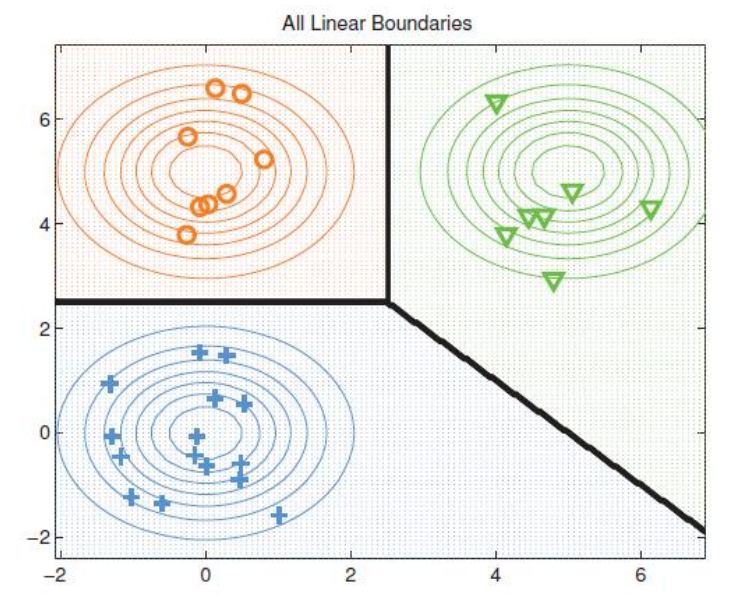
我们可以看到,多元高斯分布分类器(判别器)的模型参数就是高斯分布的参数:
,基于上一节的结论,直接使用极大似然估计来计算参数。
先计算对数似然函数,其即是 对每个分类的多元高斯分布 做 加权平均(没错这和离散情况的下的贝叶斯分类器其实是一样的):
右侧的N即为类别c对应的多元高斯分布的概率密度函数。
而表示第c个类的先验,其满足以下条件:
在实际使用时,往往以每个类c在数据集中的统计频率结果作为先验,带入极大似然估计可以得到,第c个类的多元高斯判别器参数为:
其中,是类别c的样本在数据集中出现的次数。
多个正态分布的高斯混合模型
上面的单一正态分布模型,看起来很美好,但是存在一个问题:我们假定了任何一个类别c的数据都只服从一个单一的正态分布
事实上,我们无法假设任何要拟合的连续数据都真的只服从一个正态分布。
实际很多情况下, 真实的数据是 多个不同正态分布的叠加。
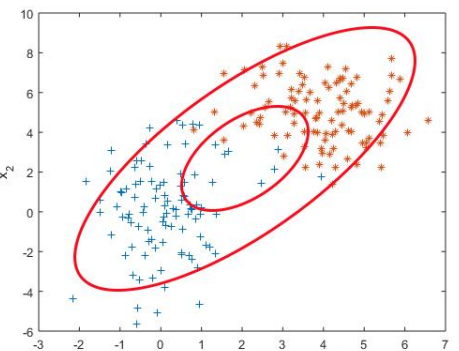
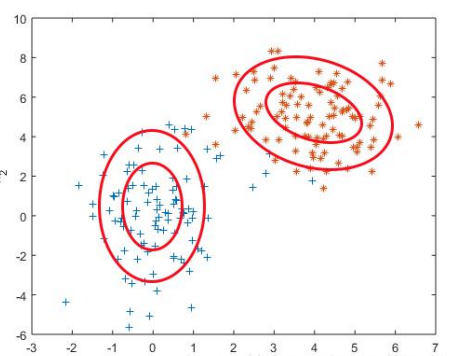
因此,我哦们需要——高斯混合模型:

理论上来说,高斯混合模型可以模拟任意的分布函数。
为了能对数据进行 “混合高斯建模”,首先我们需要知道要建模的数据空间到底需要几个正态分布的类。
没错,所以建立高斯混合模型的第一步,是聚类(clustering)。
这就和上一节的生成分类器很不一样,前者我们已知(假设了)每个类别对应一个正态分布。而在这里是不同的,我们不能相信标签里的类别信息,只能将最终每个类别需要混合的正态分布的数量视为隐变量。
EM算法 估计高斯混合模型
我们依然可以写出MLE方法和MAP方法对混合高斯模型的对数似然函数:

最大的问题在于:我们不知道隐变量z(即真实正态分布的分类数量)的维度,因此参数的解也是不唯一的。
如果我们假设有k个维度(即每个分类用k个正态分布混合表示),那么就会有k!种不同的解。
把k也加入模型的参数中,我们可以用C4中提到变分EM算法来进行最大似然估计。
公式的推导很长,如何以后有机会的话我把它整理一下放到另一个链接里……
这里我们简单回顾一下过程吧:
- 1、定义Q函数,步数t=0,定义一个初始先验。然后每一步迭代推导隐变量的条件概率
- 2、E步:计算t-1步中,将Q函数表示为多元正态分布的参数
- 3、M步:最大化Q函数值,结果作为下一次迭代的参数。
- 4、重复2-3步
下图是一个实际迭代过程的可视化举例:
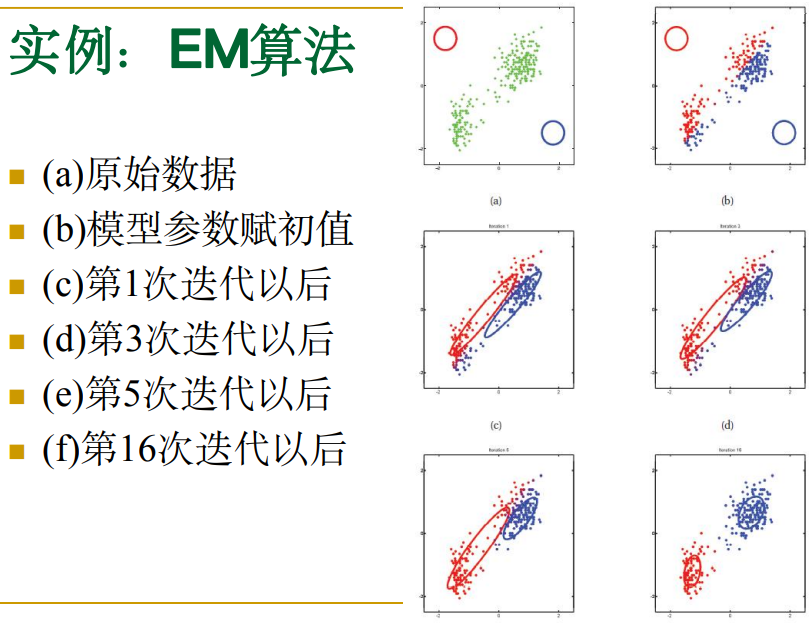
K-means算法 估计高斯混合模型
你们可能在数据分析或者数据挖掘课上学到过K-means算法,你们有没有好奇过,这个算法的原理到底是什么?
天哪如果你只看上一节就敏锐地发现了其实K-means算法就是EM算法的近似变形的话那你可太NB(朴素贝叶斯)了,我上课的时候是一点没听懂,感觉这还是八竿子打不着的两个问题……
K-means算法其实是上述 混合高斯模型估计的 一个近似特例。
直观地说这么解释:它们在聚类的时候其实都是一开始未知类别的数量k,然后通过计算不断收敛的。
它做了两个假设:
- 每个要混合的正态分布的 协方差矩阵 已知 (假设它们都等于标准的方差)
- 每个要混合的类别的 先验 已知(假设它们都相等,即为1/k)
因此,在K-means算法中,我们只需要计算样本相对于每个先验点的均值,并以此来迭代估计出每个类别的分布:

好处显而易见:计算非常方便快捷,能在最短的时间得到收敛的聚类。
但是,因为做出了协方差和先验的假设,最后得到的高斯分布就再也不能用于进行概率密度估计了。因此K-means相对于直接建模混合高斯分布有以下缺点:
- 无法计算某一个样本点属于某个高斯分布类的概率值
- 因此,也就无法生成新的样本点
综上,K-means算法在数据分析中非常常用,但是它不能作为一个生成模型来使用。遗憾退场。
隐马尔可夫模型
隐马尔可夫模型是关于 时序 的概率模型 。
为此,首先你需要知道 马尔可夫过程 和 马尔可夫链 的基本定义。我假定你已经学过了《随机过程》……
什么,你没有学过?!这下可不好办了……咳咳……
问题不大,你只需要先记好这两点:
- 马尔可夫过程 是基于时序的,它假定随机变量的每个取值都随 **时间 **而变。
- 齐次马尔可夫过程 假定 每一个时刻 随机变量的概率取值 只与 上一个时刻的随机变量有关。
你不足需要知道 齐次 是什么意思,总之在本篇的应用范围内,我们可以认为马尔可夫过程都是齐次的。
这样的一个过程中,状态组成的序列被称为马尔可夫链,因为每一个时刻都是可以和上一个时刻通过概率相连的。
而在隐马尔可夫模型中, 状态序列(state sequence)是隐藏的,从外部数据无法观测。这也就是为什么被称为隐马尔可夫链。
那么外部观测的是什么呢?我们只知道它和当前时刻的那个隐藏状态有关。我们把每个时刻中观测到的数据也组成一个序列,称为观测随机序列 (observation sequence )
这样一定很不好理解,问题不大,我们来举一个例子:
骰子游戏
- 假设有三个不同的骰子:D6、D4、D8 (六面、四面和八面骰子)。
- (——为什么没有D100?!——兄弟你走错片场了,这里玩的是DND)
- 每次投掷前,先等概率地随机从三个骰子中选取一个。
- 然后投掷选到的骰子,骰子随机地产生一个数字。
如果我们每次记录下每次得到的数字,那么它们就组成一个观测序列。
隐藏序列是什么?是我们每一次投的是哪一个骰子。
加入我只告诉你前面几次投掷的结果是:1 6 3 5 2 7 3 5 2 4 ,要估计下一次投掷的结果,那么隐藏状态必然是猜测下一次骰的是哪一个骰子。

接下来我们就以这个“生成骰子游戏点数”的模型为例子,来介绍隐马尔可夫模型。
隐马尔可夫模型 有三个要素:
- 初始概率分布 :即第一次(0时刻)观测变量的概率分布
- 如骰子游戏中,第一次试验可能得到1-8中的一个数字,可以通过组合方法计算出初始分布。
- 比如,第一次试验产生数字1的概率
- 如骰子游戏中,第一次试验可能得到1-8中的一个数字,可以通过组合方法计算出初始分布。
- 状态转移矩阵:每个隐藏状态在下一时刻可能转换为另一个隐藏状态的概率:
- 在骰子游戏中,三个骰子被视为三个隐藏状态。
- 其中,每个状态在下一时刻都有等概率(1/3)转变为任意的三个状态(包括它自己)
- 观测概率矩阵 :从每个已知隐藏状态到观测状态的概率
- 在骰子游戏中,_(如果t=0)_对于D4,每个观测状态(1-4)的概率是25%,其他三个骰子类似。
将马尔可夫过程的假设写成数学公式,就是:
1、齐次马尔可夫性假设
隐马尔可夫链 **时刻的状态 只和 **时刻的状态 有关, 与其他时刻的状态及观测无关,也与时刻无关 :
2、 观测独立性假设
观测变量只和当前时刻的状态有关,与其他时刻的 观测和状态均无关
在骰子游戏中,观测变量是离散的,因此模型参数可以使用多项分布或贝塔分布,如果观测变量是连续的(如语音或文本),可以使用上面几节介绍的多元高斯分布来建模。
但是 **状态空间 **在隐马尔可夫模型中 一定是离散的
根据任务的不同,隐马尔可夫模型要求解的问题可以被分为以下几类:
- 学习:已知观测序列,学习模型参数,使得生成该观测序列的概率p最大
- 解码(预测隐空间):给定模型参数和观测序列,求最有可能的隐藏状态序列
- 计算(预测观测结果):给定模型参数和观测序列,求该观测序列生成的概率。按照是否已知整个序列的数据,还可以分为:
- 前向算法(在线学习):已知中间观测序列1-t,求生成到该序列的概率:
- 后向算法(离线学习):已知整个观测序列1-T,求
可观测隐变量学习
在骰子游戏这个例子中,虽然从给定的观测序列中我们无法知道隐变量的分布**,但是我们知道隐变量定义为三种骰子的随机选取,它服从某种特定的规则。**
类似这种情况,我们仍为隐变量z仍然是可观测的,因此,可以直接利用极大似然估计法来估计隐马尔可夫模型参数 。
对于N个状态序列的离散变量,我们可以使用多项分布建模: 假设观测变量x服从多项分布,其中k表示隐藏状态,l表示观测到的序列:
我们在C2章已经举过例子了,不如推导留给你们,这里是参数和 A 的估计结果:
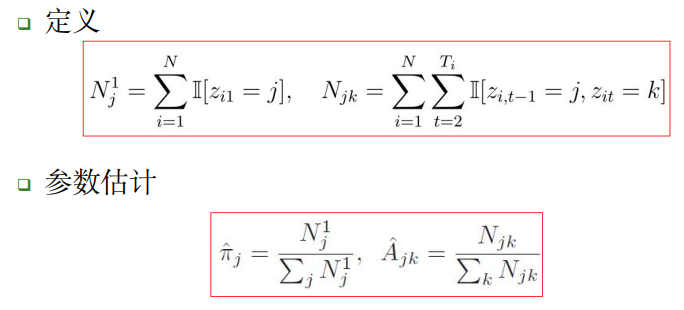
而参数矩阵B则使用统计方法计算:
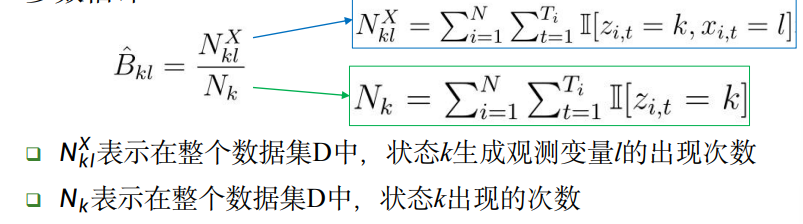
如果 观测变量x服从正态分布,那就如同前面几节的方法,如法炮制, 在计算观测概率B时,将分子分母替换为 均值 和 协方差 矩阵即可。
不可观测隐变量学习
那么,更多的情况下,我们确实无法观测隐变量z,或者无法得知其的生成规律,此时我们需要一种 非监督的学习方法
Baum-Welch算法 :一种改进的EM算法,用来解决隐马尔可夫模型的参数估计。
老三样:
- Q函数:
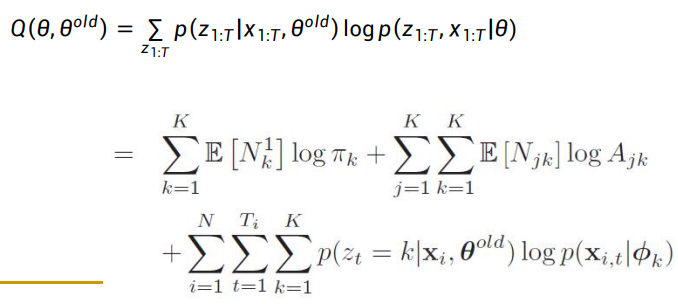
这里因为符号t已经被用来标记马尔可夫过程的时刻,我们用old上表标记参数的上一次迭代。
- E步:在这里我们需要计算数据集中已知的序列在当前参数下的生成概率,具体方法参见后面的“计算问题”小节。

- M步:


计算问题
- 前向算法 :从第0步开始,算出下一步的概率密度

- 我们可以发现,t时刻的隐藏状态依赖于t-1时刻的隐藏状态,利用马尔可夫链的特性,我们可以定义下面的两个转移函数,其中i,j都是某一个隐状态:
- 定义t时刻的 信念状态 (belief state):

- 于是我们得到:其中是所有转移函数组成的矩阵,并由此可以从t=1开始计算信念状态,从而得到最中的概率密度链
- 后向算法: 与前向计算相反,使用 条件似然函数 从最终时间T(前提:我们知道整个序列)反向推导每个时间点的序列概率。
预测问题
假设我们已经知道了模型参数和观测得到的序列数据,现在,我们想要推断最有可能的隐状态序列:
我们可以从第一个时刻起,每个时刻取的隐状态z标记一个代价:即 前面所有步骤的计算概率是否最大:
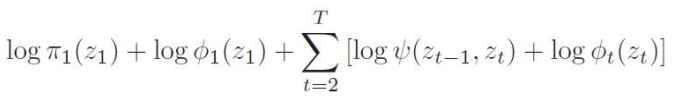
这样,我们就将求隐状态序列转换为一个 最大(优)路径问题。
然后,我们可以使用计算机算法来求解,例如贪心算法。
下面介绍一个称为 维特比算法 的方法,它的思想是用 动态规划 解最大路径问题:
- 从终结点开始,由 后向前逐步求得结点 ,得到最优路径