C2 离散数据的生成模型
C2 离散数据的生成模型
生成模型的目的:学习联合概率分布 P(X,Y)结合第一节课的知识,接下来我们会介绍一些比较传统的生成模型,它们不会涉及DL和神经网络,但是是后续生成模型的数学基础。
贝叶斯概念学习(以离散模型举例)
只提供正向的样本,让模型学习正向的特征,然后判断输入是否属于要训练的类别(概念)
与二分类任务的原理相同,但是训练二分类模型会提供 both 正向样本和负向样本
**以学习一个猜数字的模型为例:**问题:有一个由数字组成的数据集,问如何学习一个概念C(C是未知的,描述数据集中数字应该服从的分布),这里的数字都在0-100之间。
- 假设空间:人为地提出“假设”,用来猜测概念C。根据某一个概念假设(如“偶数”),所有可能生成的元素组成h的集合。比如“偶数”,则对应的假设数据集。所有可以提出假设组成假设空间
- 版本空间:即所以“有效的”假设组成的空间。即满足:数据集D中的所有元素在假设的集合h中,这些假设组成的空间。
注意:一般来说,数据集D中包含的元素数量越多,版本空间就会越小,因为会有很多假设连数据集中的采样数据都过不了关,就被筛除了。
- 似然(likehood):从h中独立采样N次,从假设能生成 数据集D中数据的概率
, 这里|h|表示h的集合大小
考虑假设1:h=“偶数”,假设2:h=“2的幂”
- 若 D = {16},则假设1的概率P(D|h) = 1/6,则假设2的概率P(D|h) = 1/50
- 若 D = {2,8,16,64}
- 此时,假设2 的 似然概率是 假设1 的4812.5倍
- 奥卡姆剃刀原则:选择似然相近的假设时,假设h中包含的数据数量越少越好
- 先验概率:当提出假设时,为其中的数据赋予先验概率 。当提出的假设在数据集中对应的实际意义不太自然时,为其赋予低的先验概率
比如,D = {50,60,70,90},给与两个假设,分别包含数据 67 和 210
如果数据集描述的是自然数,那么包含210的假设拥有更高的P(h) ,因为210和D中数据都是10的倍数
如果数据集描述的人的体重数据(kg),那么包含67的假设拥有更高的P(h),因为210在不太可能是符合概念的数据
- 后验:判断版本空间中的概念谁更接近要学习的概念。根据贝叶斯公式,后验概率与 先验概率和似然的乘积成正比:$$P(h|\mathcal {D}) \propto P(\mathcal {D}|h) P(h)$$,后验概率最大的假设可以被认为是最优假设。
- 如果用H标记假设空间中所有假设i组成的集合,那么将数据集D与每种假设的联合概率求和,就是后验概率的基数了,即:
注意:预先定义的假设空间不一定是完备的,真·概念C不一定在你的空间中,如果这样(现实中大多数情况也是如此),找到的最优假设只能说是最接近C的。
接下来我们尝试直接用数学推导出求最大后验概率的公式:
- 最大后验概率估计 MAP
- 我们要求一个h,其会使得后验概率最大,数学中我们用argmax函数来描述使得一个函数取最大值时,自变量的值,因此:
- 分母对所有假设的联合概率求和,这与h无关,因此我们可以认为:
- 右边我们取对数,在不破坏函数的单调性的同时将乘积的概率变为加法,然后我们会发现:
- 常量N会影响最大函数的取值
- 当N越大,即数据足够多时,即的对数增长速率远大于
- 因此在计算出最大概率的h时,后者影响越来越小,直到可以忽略不计,因此,在实际建模中,我们常常只估计似然,我们将这种近似的方法称为:极大似然估计 MLE :
\hat{h}^{mle}\ \~= \ argmax_h \ P(\mathcal {D}|h) = argmax_h \ log([\frac{1}{|h|}]^N)
于是,当N足够大时,将每个H空间中的假设h代入上式,使得函数取值最大的h可以被视为最优假设。
- 生成新数据:已知最优假设h后,便可以直接以该估计作为条件,求出生成各种元素(x)的概率:
以上是一个离散分布的贝叶斯概念模型学习的例子,根据概率论,这个方法也可以推广到的连续随机变量的情况,比如服从二项分布的概率模型。相应地,我们需要将计算似然和概率估计的概率P(X)改为概率密度p(x),而将求和计算转为积分。下面会介绍两个连续分布的贝叶斯概念模型
Beta二项分布生成模型
现在来看连续随机变量的情况,以抛硬币的二项分布为例:
- 抛一个硬币N次,记录有次正面朝上,次反面朝上
- 假设每次抛硬币的结果为随机变量x,x服从二项分布,正面朝上记为1,反面朝上记为0
- 那么,二项分布的参数(正面朝上的概率)在[0,1]之间,是一个连续变量,也是我们要估计的
注意:我们的目标是估计的分布,而不是直接求出一个结果(不然直接频率作为概率不就完了,不行,你这不贝叶斯啊)。
因为有很多可能的,都可以使得我们的抛硬币实验得到上述的结果。
我们现在已知N次独立实验的结果,次正面朝上,次反面朝上就是“数据集”的数据,因此可以写出已知采样与我们实际要求的“抛硬币哪一面向上”分布的似然:
- likehood:$$P(\mathcal {D} | \theta) = \theta{N_1}(1-\theta){N_0}$$
记住我们要求后验概率,它等价于先验概率和似然的乘积。现在的问题在于:我们怎么知道先验概率?我们可以用贝塔分布来作为我们的先验概率模型,之所以是它的理由如下:
- 贝塔分布常用于估计[0,1]分布上,缺少足够先验样本的分布
- 贝塔分布有一个重要的特性:共轭先验,即将其带入贝叶斯模型,得到的后验概率的函数形式与先验相同。而如果我们将独立实验的结果或次作为随机变量计算先验,其服从伯努利分布,似然函数的形式也与贝塔分布的先验相同。
我们假设先验服从贝塔分布:于是我们现在可以计算后验:
现在,我们只需估计后验函数取尽可能大值时,参数θ的分布,根据贝塔分布的特性,
Beta(a,b) 分布的随机变量取最大值时,参数为
得到最大后验概率估计:,根据共轭先验的性质,我们要估计的分布也是一个贝塔分布,其具体形状与参数a,b有关。
- 如果我们使用极大似然估计,即不考虑先验,则结果退化为:,即直接用频率估计概率的结果,如果我们取上述贝塔分布的a=b=1(均匀分布,认为先验的结果硬币正面朝上的概率就是五五开的),那么也会得到这个结果。
使用MAP的结果,我们可以生成下一次抛硬币正面朝上的结果估计:
可以发现,结果正好是我们的贝塔分布模型的均值。有趣的是,只要我们使用MAP的生成结果,即使取a=b=1的均匀分布,也会使得估计正面朝上的概率中,分子至少为1,不会出现 _因为实验数据集中没有正面朝上,就将其判定为不可能事件 _的情况。因此,这种方法也被称为**”(拉普拉斯)+1平滑“**
狄利克雷多项分布生成模型
再来看一个复杂一点的情况:随机变量有K个可能的取值,比如说,估计一个有k面的骰子,每个面朝上的概率。我们假设做了N次实验,每个面朝上的次数分别为:和伯努利实验类似,可以这样定义:
- 似然函数:
- 先验函数,将之前贝塔分布的共轭先验推广到多个变量,这就是狄利克雷多项分布:
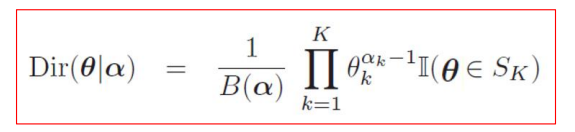
- 后验计算:

- 最大后验概率估计:
- 同样的,如果使用最大似然估计,会退化为:
- 生成一个骰子点数,其结果是j点的概率:
朴素贝叶斯分类器(NBC)
在第一章,我们说了 生成模型 包含 分类模型的所有功能。比如下面这个分类问题:
将若干个由离散数据组成的向量进行分类。设变量 是长度为D的特征向量,每个元素(特征)有个可能的取值,希望将所有这样的向量分为C类: {1,2,…C} ,用 Y=c 来表示结果的类标号。于是我们想要知道,给定向量x和模型参数向量θ,分类的概率:,只要对所有的类别c计算这个概率,取最大值作为最终分类。
我们尝试用贝叶斯生成模型的方法来解决这个问题。这涉及到刚才两节二项分布和狄利克雷多项分布方法的综合。
首先,我们考虑给定类别c,能生成特征向量x的概率:
则由贝叶斯公式,要求的概率可以表示为:
可以发现,因为现在问题空间包含两个随机变量x,Y,对于类别的变量Y,式子中也推出了先验概率。
就是分类先验(在训练的数据集中,最终被每一类被分入了多少个向量)。
这会使得模型的参数向量θ中还要包含分类先验的参数。如果将它们和向量x的参数混为一谈,这将导致无法更新参数。为了能将向量内的每个特征对应的参数拆分出来计算,朴素贝叶斯提出一个重要的假设:
给定同一个类别的标签,每一个特征的条件都是独立的
注意:真实世界中,这个假设是很难成立的,但是依然该方法依然可以用来估计分类器
则我们可以将特征向量在模型中的参数用θ表示,而分类先验的参数在下文将用来表示,它们将被分别估计。先来看特征向量:
我们用来标记以 向量中的每个特征 为随机变量的 分布。对于特征的定义不同,这个分布会表示成不同的形式:
- 如果特征是0-1编码的:值不是0就是1,那么是伯努利分布,参数要表示 第i个特征的值会使得整个向量有多大可能性落在分类c中
- 如果每个特征有个可能的取值(原始的问题),那么是多项分布,参数要表示为一组向量。
- 如果特征是连续的实数来表示的,那么将是一个连续的高斯分布,参数也要表示为<均值,方差>的一组值。
回到问题的开始,为了下面的推导写的比较简单,我们将问题简化为只要0-1编码的两种特征
(它已经很复杂了QAQ,再加上K个类别我都不敢想……)
然后我们来看看如何使用贝叶斯学习来进行训练:假设训练数据集中包含了N个**<向量x, 分类标签Y>**的数据对,每个对用来表示,那么分类的先验表示为:$$P(Y_i|\pi) = \Pi\ \pi_c^{if(Y_i =c)}$$
- 表示计数函数,即只有第i个分类标签为c时,才保留参数【没错,还是统计方法】
- 注意这里作为条件概率的pi和下面的θ都是向量,而右侧式子表示取向量中的哪一个有效值(用符号来区分 分类的参数向量 和 特征的参数向量)
同样,特征的先验计算为:
于是,推导整个数据集的后验概率函数,即将所有数据的结果相乘起来:
尝试使用极大似然估计来直接计算参数(MLE),直接对两边取对数,得到:
(其中表示向量中的第个值)上面的式子看着非常复杂,其实本质上与上一节的二项分布估计相同:
- 分类的先验估计就是:从数据集N中统计出分类c出现次数,并计算比例:
- 特征的似然参数估计就是:从每个已知类别的出现次数中,统计出是当前特征的比例,即:
- (不是0-1编码的,就是一个嵌套的向量了)
这个结果,与抛硬币和骰子一样,因为先验是完全按照统计结果的,容易出现过拟合的问题。另一种方法,可以使用刚才的贝叶斯方法,对pi和θ两个参数的分布假设先验:
:::warning
- 假设是一个狄利克雷分布,参数是
- 假设每个 都是一个贝塔分布,参数是
:::
然后计算后验,形式是一样的,只不过丑陋的计数函数被替换成了先验分布的均值: 代入最大后验概率估计MAP的估计结果是:
代入最大后验概率估计MAP的估计结果是: 如果有一条新的数据需要分类,那么对于每个类别,将MAP估计的参数带入,得到使得概率最大的c就是要求的分类。可以看出,朴素贝叶斯模型虽然推导起来比较复杂(其实也只是复杂在数据维度比较多,人脑CPU容易干烧,交给计算机来还是很快的),但是计算复杂度很低,所以在小场景中使用广泛。同时,我们也可以用这个模型生成新的数据:和二项分布生成模型一样,在生成新的数据时,代入模型的参数就是分布的均值:
如果有一条新的数据需要分类,那么对于每个类别,将MAP估计的参数带入,得到使得概率最大的c就是要求的分类。可以看出,朴素贝叶斯模型虽然推导起来比较复杂(其实也只是复杂在数据维度比较多,人脑CPU容易干烧,交给计算机来还是很快的),但是计算复杂度很低,所以在小场景中使用广泛。同时,我们也可以用这个模型生成新的数据:和二项分布生成模型一样,在生成新的数据时,代入模型的参数就是分布的均值:
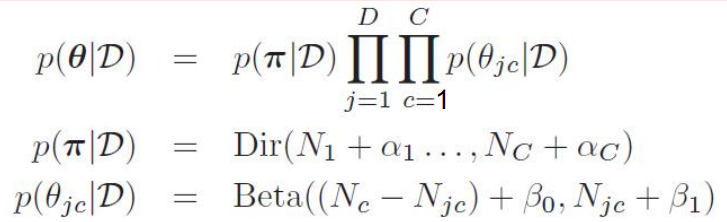 代入最大后验概率估计MAP的估计结果是:
代入最大后验概率估计MAP的估计结果是: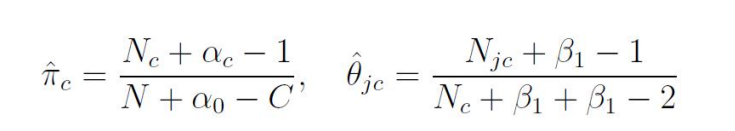 如果有一条新的数据需要分类,那么对于每个类别
如果有一条新的数据需要分类,那么对于每个类别