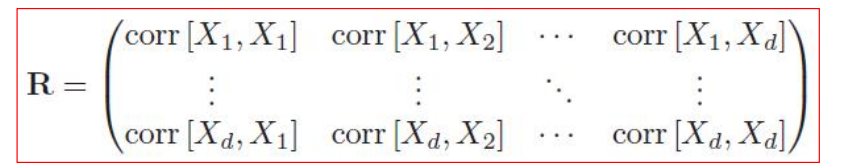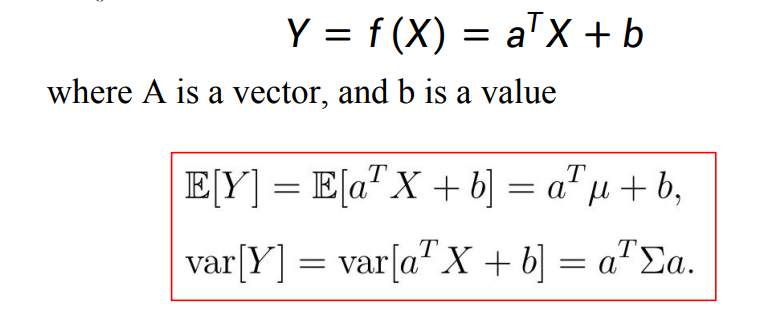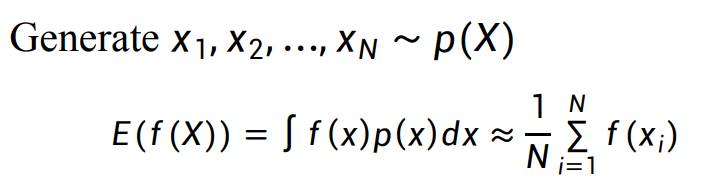【笔记】生成模型基础与应用 - 第1章

C1 概率论和统计基础

C1 概率论和统计基础

什么是概率？

• 频数的概率解释：频率估计概率（小学就学过的）
• 贝叶斯概率解释：概率是某样事件的“不确定度”，是人们在多大程度上相信某件事情将会发生（似然likehood）
  • 因为贝叶斯概率能适用更多更广泛的概率事件（例如：从未发生但可能的事件），因此以下讨论的概率偶都基于贝叶斯概率

事件、随机变量和概率分布：

• 事件：自然语言描述的具有随机性的事件
• 随机变量：可能从有限 或 可数的无限 集合X中随机取值的变量
• 概率的表示：P(事件A) = P(随机变量X=某值a) 【如果我们定义当X取a时事件A发生】
• 概率分布：表述随机变量X的 取值 的 概率规律 的集函数

离散随机变量要点回顾

• 事件合并概率：
  • $P(A ∪ B) = P(A) + P(B) - P(A ∩ B)$
  • 如果A和B是互斥事件，则：$P(A ∪ B) = P(A) + P(B)$
• 两个随机变量的联合概率：
  • $P(A,B) = P(A)P(B|A) = P(B)P(A|B)$
• 联合概率分布的链式法则：

$P(X_1,X_2,...,X_D)=P(X_1)P(X_2|X_1)P(X_3|X_1,X_2)...P(X_D|X_1,X_2...X_D)$

• 两个随机变量的条件概率：

$P(B|A) = \frac{P(B,A)}{P(A)}=\frac{P(B)P(A|B)}{P(A)} \ ,P(A) > 0$

• 贝叶斯条件概率公式

• 重要名称：

  • 先验：已知的，B事件发生的概率
  • 似然：在B的条件下A发生的概率 与 A发生的概率 之比：$\frac{P(A|B)}{P(A)}$
  • 后验：在A的条件下，B发生的概率，即P(B|A)

• 两个随机变量的条件独立性：

  • 如果两个变量的联合概率可以被拆分为各自概率的乘积，则称两个变量是 （无条件）独立的
  • $P(X,Y) = P(X)P(Y)$
  • 而如果给定随机变量Z，在Z的条件概率下满足上述条件，则称两个变量X,Y是 条件独立的
  • $P(X,Y|Z) = P(X|Z)P(Y|Z)$

连续随机变量要点回顾

• 累计分布函数（cdf）：F(x) = P(X <= x)当连续变量的取值小于x时，总计的概率

  • 概率密度函数（pdf）：p(x) = F(x) dx 是累计分布函数的微分
  • 计算连续随机变量在a,b区间上的概率：F(b) - F(a)，或是在p(x)上积分

• 连续分布的数学量：均值E、方差σ^2、中位数……

• 协方差：对于两个随机变量X,Y，衡量它们的线性相关性：

  • $cov[X,Y] = E[(X-E(X))(Y-E(Y))] = E(XY) - E(X)E(Y)$

• 相关系数：将协方差标准化后的数学量：

  • $corr[X,Y] = R= \frac{cov[X,Y]}{\sqrt{\sigma^2(X) \sigma^2(Y)}}$

• 独立的两个变量，它们不相关
• 但是，不相关的两个变量，可能互相独立
• 如果两个符合高斯分布的变量不相关，则它们一定独立

• 对于多元随机变量的联合分布，协方差和相关系数的计算将变为矩阵的形式：
  • 
  • 

常见概率分布回顾

【离散的】

• 经验分布（eCDF）：描述从抽样中得到的概率分布，经验分布的概率密度函数即为所有抽样的结果之和，其中抽样被定义为 狄利克雷函数：即抽样的结果只有0或者1.

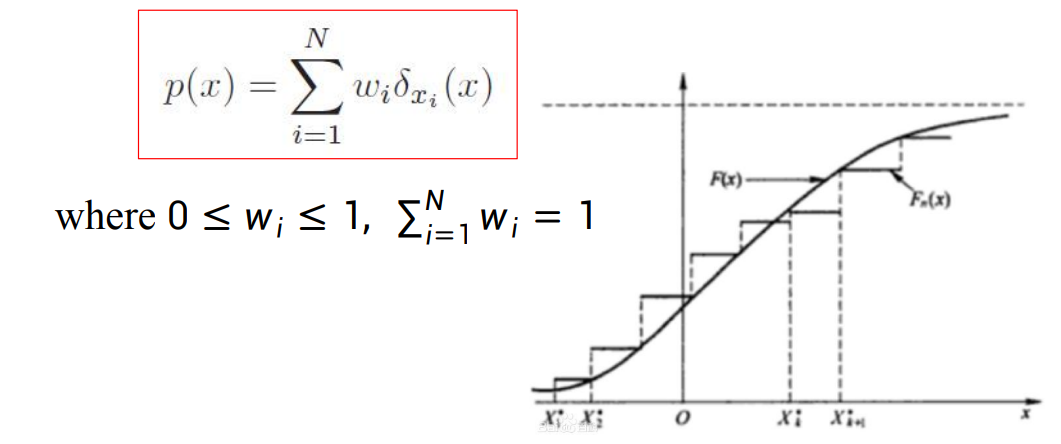
• 二项分布：重复n次独立的 伯努利事件 实验，获得其中一种结果k次的概率分布
  • 伯努利事件：某个事件只有两种可能的结果（布尔随机变量），其中一种的概率为p，另一个为1-p
  • 经典的例子是抛硬币
• 多项分布：重复n次独立的 多重伯努利事件 实验，获得 每种结果的次数 的概率分布
  • 多重伯努利事件：某个事件可能有k种不同的结果，并且每种结果具有固定的概率
  • 经典的例子是投一个k面的骰子

【连续的】

• 均匀分布：在一个区间或域上，随机变量的取值为固定值
  • 对于一维变量，随机分布的概率密度函数为：$Unif(x) = \frac{1}{b-a} (a \leq x \leq b )$
• 正态分布（高斯分布）：多个相互独立的随机变量之和 的分布 会趋近于这个分布，因此它被广泛使用
  • 正态分布的概率密度函数和符合该分布的随机变量的均值和方差有关
  • $N(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{1}{2\sigma^2}(x-\mu)^2}$
  • 可以拓展为多元变量的正态分布，将均值修改为多元变量的数学期望，方差修改为多元变量的协方差
• 泊松分布：对二项分布的连续近似，在二项分布的实验次数n很大，单次概率p很小时，二项分布可被近似为泊松分布。
  • $P(x|\lambda) = e^{-\lambda}\frac{\lambda^x}{x!}$, 其方差和均值都是 λ
• Student t 分布：基于正态分布，为了增强其抗干扰性而提出的分布，加入一个参数v：
  • 
• 拉普拉斯分布（双指数分布）：在均值的两侧，呈现对称分布规律的一种 指数分布 变种
  • $Lap(x|\mu,b) = \frac{1}{2b}e^{-\frac{|x-\mu|}{b}}$，其均值为 $\mu$，方差为 $2b^2$
• 伽马分布：对正实数域上的随机变量建模的分布，是多个独立同分布的指数分布变量 和 的分布
  • $Gamma(x|a,b) = \frac{b^a}{\gamma(a)}x^{a-1}e^{-xb}$，其中γ(a)是伽马函数：\gamma(a) = \int_0^\inf t^{a-1}e^{-t}dt
  • 参数a被称为shape，b被称为rate，该分布均值为 $\frac{a}{b}$，方差为$\frac{a}{b^2}$
• 贝塔分布：对[0,1]区间上取值的随机变量建模的分布
  • $Beta(x,|a,b) = \frac{1}{\beta(a,b)}x^{a-1}(1-x)^{b-1}$,其中 $\beta(a,b)$是贝塔函数，它只是为了使得这个分布的概率密度积分等于1才加上的。
• 狄利克雷分布：将贝塔分布拓展到多元变量的泛化
  • 

【分布的变换】
若分布Y可以由服从分布X的随机变量，将每个取值用离散或连续的函数f变换得到，那么分布Y的均值和方差会遵循以下公式

• 线性变换：
  • 
• 通用变换：
  • 离散变量：
    • $p_y(y)=\sum_{x:f(x)=y}p_x(x)$
  • 连续变量：
    • $p_y(y)=p_x(x)|\frac{dx}{dy}|$

其他重要概念

• 大数定律：随着样本规模的增加，样本均值对总体均值的估计越准确。
• 中心不变定理：多个随机变量样本的均值分布（随机变量和的分布）将近似于高斯分布。
  • 
• 蒙特卡洛近似：如果某随机变量X的分布未知，但可以对其进行抽样来实验，则可以使用经验分布来近似X的分布：
  • 
• 衡量两个分布的相似度（距离）：KL散度
  • 先补充信息论的知识：信息熵
    • 信息熵可以描述随机变量X在分布P上的不确定性的程度：$H(X) = -\sum_K^{k=1}p(X=k)log_2p(X=k)$
    • 均匀分布的信息熵最大
  • 交叉熵：将服从分布P的变量转换到分布Q，需要提供额外信息（bits）的量，其中p和q代表P和Q的概率密度函数
    • $H(p,q) = -\sum_{k}p_klogq_k$
  • KL散度：描述两个分布的概率密度函数p和q的相似度：
    • $KL(p||q) = \sum_{k=1}^Kp_klog\frac{p_k}{q_k}=-H(p)+H(p,q)$
  • 互信息度：衡量两个分布的变量之间互相依赖的程度：
    • $II(X;Y) = KL(p(X,Y)||p(X)p(Y))\ = \sum_x\sum_yp(x,y)log\frac{p(x,y)}{p(x)p(y)}\\=H(X)-H(X|Y)=H(Y)-H(Y|X)$